Evolutionary Multi-agent System
In the approaches applied to evolutionary algorithms, the exact course of evolutionary processes depend on some context of a particular individual or subpopulation (e.g. the location in the population structure). The idea of decentralised model of evolution realised as an evolutionary multi-agent system may be considered as a step further in that direction.
Agents of EMAS represent or generate solutions for a given optimisation problem. They are located on islands (representing distributed structure of computation), which are their local environment, where direct interactions may take places. Obviously, agents are able to change their location, which allows diffusion of information and resources all over the system.
In EMAS phenomena of inheritance and selection – the main components of evolutionary processes – are modelled via agent actions of death and reproduction. Inheritance is accomplished by an appropriate definition of reproduction, like in classical evolutionary algorithms. Core properties of the agent are encoded in its genotype and inherited from its parent(s) with the use of variation operators (mutation and recombination). Moreover, an agent may possess some knowledge acquired during its life, which is not inherited. Both inherited and acquired information determines the behaviour of an agent in the system (phenotype).
Assuming that no global knowledge is available (which makes it impossible to evaluate all individuals at the same time) and the autonomy of the agents (which makes reproduction be achieved asynchronously), selection is based on the non-renewable resources. It means that a decisive factor of the agent’s fitness is still the quality of solution it represents, but expressed by the amount of non-renewable resource it possesses. In general, the agent gains resources as a reward for ‘good’ behaviour, and looses resources as a consequence of ‘bad’ behaviour. Selection is then realised in such a way that agents with a lot of resources are more likely to reproduce, while the low level of resources increases the possibility of death. So according to classical Franklin’s and Graesser’s taxonomy – agents of EMAS can be classified as Artificial Life Agents (a kind of Computational Agents).
In EMAS, explicitly defined living space facilitates an implementation in a distributed computational environment. The population of individuals may be easily decomposed into subpopulations connected by the means of predefined topology. Thus, genetic material may be exchanged among the subpopulations (similar to classical niching technique - allopatric speciation). Subpopulations may be assigned and run independently on remote nodes. Classical peer to peer computing, clustering or grid approaches may be further adapted.
To recapitulate: the main advantage of the approach under discussion is that it covers various specialised evolutionary techniques in one coherent model, which enables the following:
- local selection allows intensive exploration of the search space and explicitly defined living space facilitates implementation in a distributed computational environment, which is similar to parallel evolutionary algorithms
- evaluation of agents, or more generally, the way a phenotype (behaviour of the agent) is developed from a genotype (inherited information) depends on its interaction with the environment, like in coevolutionary algorithms
Figure below shows the simplest possible model of an evolutionary multi-agent system, with one type of agents and one resource (called “energy” - shown as an amount of money) defined:
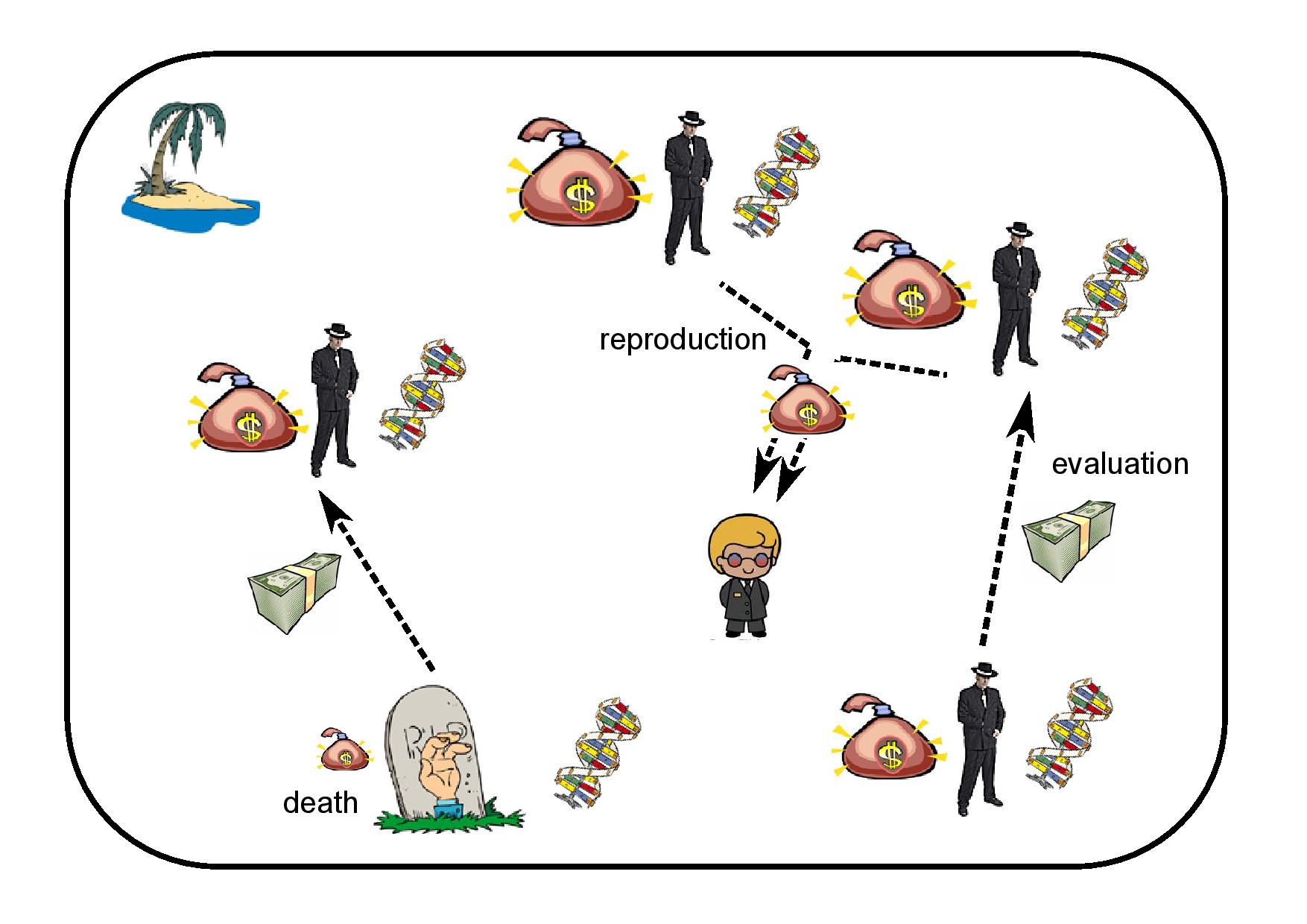
Genotypes of agents represent feasible solutions to the problem. Energy is transferred between agents in the process of evaluation. When the agent finds out that one of its neighbours (e.g. randomly chosen), has lower fitness, it takes a part of its neighbour’s energy, otherwise it passes part of its own energy to the evaluated neighbour. The level of life energy triggers the following actions:
- Reproduction – performed when the agent’s energy raises above a certain level, followed by production of a new individual in cooperation with one of its neighbours, with genotype based on parents’ genotypes (crossed over and mutated) and part of energy also taken from its parents.
- Death – the agent is removed from the system when its energy falls below a certain level, the remaining energy is distributed among its neighbours.
- Migration – the agent may migrate when its energy rises above a certain level, then it is removed from one evolutionary island and moved to another according to predefined topology.
Each action is attempted randomly with a certain probability, and it is performed only when their basic preconditions are met (e.g. an agent may attempt to perform the action of reproduction, but it will reproduce only if its energy rises above certain level and it meets an appropriate neighbour).
Global optimisation task is usually defined as a search for a value of the argument of some fitness function which gives its maximal value. The optimisation task may be classified as continuous, discrete, combinatorial, mixed or constrained. Moreover, it is easy to see that the problem of maximization may easily be changed into minimisation when needed, by negating the value of the function under consideration.
Solving optimisation problems with evolutionary algorithms requires choosing the encoding of solutions according to the search space definition, crossover and mutation operators appropriate for the encoding, as well as configuring a selection mechanism, or other components of specialised techniques like migration strategies for the island model of parallel evolutionary algorithms. The use of EMAS needs similar decisions concerning the encoding and variation operators, but the configuration of the system is different.
